Estimación del viento meteo

La estimación del viento es una característica fundamental de un computador de vuelo porque es la base para la estimación de otras cantidades como el tiempo de vuelo o la altitud necesaria para llegar a una baliza.

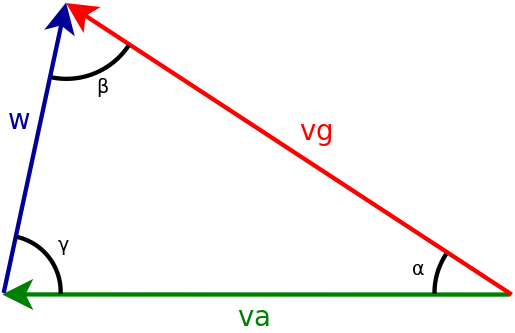
Una magnitud vectorial consta de dirección e intensidad. Un ejemplo de una magnitud vectorial es el viento. Podemos representar una magnitud vectorial con una flecha cuya longitud indica la intensidad.

• La flecha azul del gráfico superior representa el viento.

• La flecha roja representa la velocidad de nuestra aeronave con respecto a la masa de aire en la que estamos volando. Es también una magnitud vectorial cuya intensidad, que podemos medir con un anemómetro, es la velocidad aire y cuya dirección, que podemos medir con una brújula, es el curso. El curso es la dirección en la que apunta el eje longitudinal de nuestra aeronave.

• La velocidad tierra (flecha roja) es la suma de estas dos magnitudes vectoriales y por tanto es también una magnitud vectorial cuya dirección es el rumbo o dirección de vuelo de nuestra aeronave. Podemos medir la intensidad y la dirección de la velocidad respecto a la tierra con un gps.

Para obtener el viento debemos sustraer vectorialmente la velocidad aire de la velocidad tierra \(\color{black} \vec{w} = \vec{v_g} - \vec{v_a} \) pero la mayoría de los instrumentos de vuelo no disponen de un anemómetro para medir la velocidad aire. ¿Cómo se las arreglan sin él? Bueno, en realidad no estiman el viento instantáneo sino el viento meteo que es el viento promedio sin tener en cuenta las rachas de viento debidas a la actividad convectiva. Suponen que el módulo de la velocidad aire, aunque desconocido, también es constante. Con estas dos suposiciones tomando las velocidades que nos da el gps en tres instantes distintos podemos plantear un sistema de ecuaciones cuya solución es la dirección e intensidad del viento meteo.

$$\color{black} \vec{w} = \vec{v_g}^1 - \vec{v_a}^1$$ $$\color{black} \vec{w} = \vec{v_g}^2 - \vec{v_a}^2$$ $$\color{black} \vec{w} = \vec{v_g}^3 - \vec{v_a}^3$$

El superíndice representa el instante de tiempo. A primera vista podría parecer un sistema de 3 ecuaciones con cuatro incognitas con infinitas soluciones. Cada ecuación vectorial se puede descomponer en dos ecuaciones escalares con lo que no tenemos 3 sino 6 ecuaciones. Igualmente cada incógnita vectorial son en realidad dos incógnitas (la dirección y el módulo) con lo cual tenemos dos incógnitas para la dirección y el módulo del viento. Tres incógnitas más para las tres direcciones de la velocidad aire (cursos) en cada instante de tiempo. Recordemos que una de las suposiciones que hicimos fue que el módulo de la velocidad aire permanecía constante así que esa es nuestra sexta incógnita.

No quiero aburrirte con los cálculos matemáticos pero para que te hagas una idea: es como encontrar la ecuación de un plano en el espacio a partir tres puntos de él. Cuando añadimos ruido a la posición de estos tres puntos, al igual que sucede con los datos de velocidad que nos da el gps, y estos están demasiado juntos, la solución puede ser un plano muy distinto. Es lo que llamamos un problema mal condicionado. Para evitarlo utilizaremos una cantidad de puntos lo mayor posible y lo más separados posible unos de otros.

En el caso que nos ocupa equivale a tomar muestras de velocidad del gps durante un período de tiempo más largo y en direcciones de vuelo distintas. Sin embargo este período o ventana de tiempo no puede ser demasiado largo porque entonces el viento ya no será constante debido a cambios en las condiciones meteorológicas o el cambio a una zona de vuelo distinta con otras particularidades locales. Una ventana de 10 minutos es suficiente para garantizar que el viento no cambia y proporcionar una estimación fiable al mismo tiempo.

Sin embargo el viento también cambia con la altitud, a veces de forma repentina. A una tasa de ascenso de 2 m/s. en 10 minutos ganaremos 1200 m. de altitud. Altitud suficiente para que el viento cambie de manera significativa. Con una ventana de 10 minutos estos cambios pasarán inadvertidos porque el algoritmo los promediará.

Si quieres saber como la app Airspace resuelve estos problemas consulta el artículo El viento meteo