Lag-free variometer

Variometers that rely only in pressure sensor readings suffer from delays of more than 500 msg. The delay of the vario has a direct impact in pilot’s reaction time and in his learning proccess of wing reactions to thermal turbulence.

As we saw in the article altimeter calibration the formula to obtain the altitude over sea level is:

$$h=\frac{T_0}{L} * \left[ 1- \left(\frac{p}{QNH}\right)^{\frac{L\cdot R}{g}}\right]$$

To obtain the vertical speed we must take the derivative of the pressure signal with respect to time.

$$\frac{dp}{dh}=-\frac{g}{R\cdot T} * p \to \frac{dh}{dt} = -\frac{dp}{dt} * \frac{R \cdot T}{g \cdot p}$$

When used for free flight, the two most valuable features of a pressure sensor are responsiveness and precission. Newest pressure sensors improve precission in regard to oldest ones in some modes of operation because they feature an internal IIR filter that, on the other hand, reduces bandwith well below 2 Hz. For flight purposes we need at least 5 Hz of frequency bandwith and data sampling rates above 10 samples per second what makes this modes of operation unusable. Therefore we have to select a mode of operation that switches the IIR filter off worsening precission to around 25 cm (0.03 hPa). If x[n] represents the noise signal added to the true pressure at the moment nT where T is de sampling period in seconds, the derivative of the pressure readings of a static sensor would be:

$$y[n]=\frac{x[n+1]-x[n]}{T}$$

Assuming uncorrelated noise, the standard deviation (RMS) of the derivative signal is:

$$\sigma_y=\frac {{\sqrt 2} \sigma_x}{T}$$

Which in the case above gives an unacceptable RMS error of 3.53 m/s in the climb/descent rate. Low pass pre-filtering of the pressure signal before making the derivative is not an option because a low-pass filter reduces bandwith and adds delay too.

Fortunately a smartphone has more sensors. One of them is a tri-axial accelerometer which detects the accelerations of the phone. We are interested in the vertical component of the acceleration after substracting gravity. We integrate this signal over time to obtain an estimation of vertical speed and integrate it once more to obtain altitude.

Whereas differentiation enhances high-frequency noise, integration enhances low-frequency noise, commonly known as drift. To correct for this drift we use the sensor pressure readings. This is implemented with a kalman-filter that combines both signals weighting each one in inverse proportion to its RMS.

It’s relatively straightforward to obtain the typical RMS noise of both sensors from their datasheets or we can get this values from experimental data. Analysing data collected from the BMA220 accelerometer we can confirm that RMS noise is ten times smaller than that of the barometer BMP180 in the same smartphone. Furthermore we have detected a zero-point error of 0.1 m/s². This states the importance of calibrating phone sensors before making any measurement. There are a lot of apps that perform this calibration proccess or you can run a calibration inside your flight app.

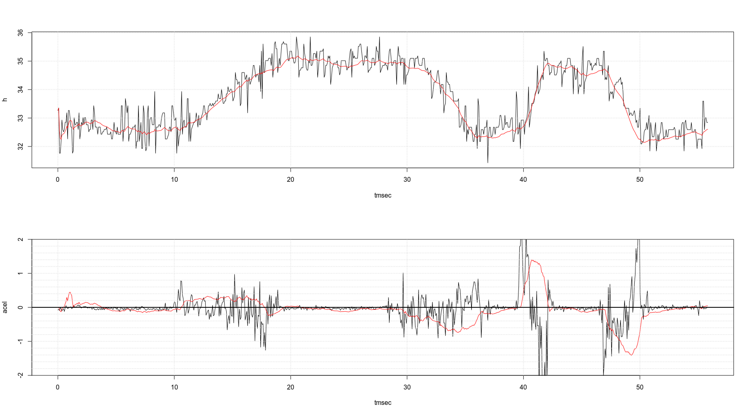
The upper plot in the figure at the header of the article represents the altitude output of the kalman filter (red solid line) superimposed to the data got from the barometer (black line). The lower plot represents the vertical speed output of the kalman filter superimposed to the data got from the accelerometer when we lift the phone two meters from the floor at 0.5 m/s and 1 m/s. Almost perfect!

However when we simulate stronger climb/descent rates arise severe inaccuracies in the accelerometer that lead to unacceptable drift in the altitude signal, and rebounds in the vertical speed signal. See the red line in the figure below.

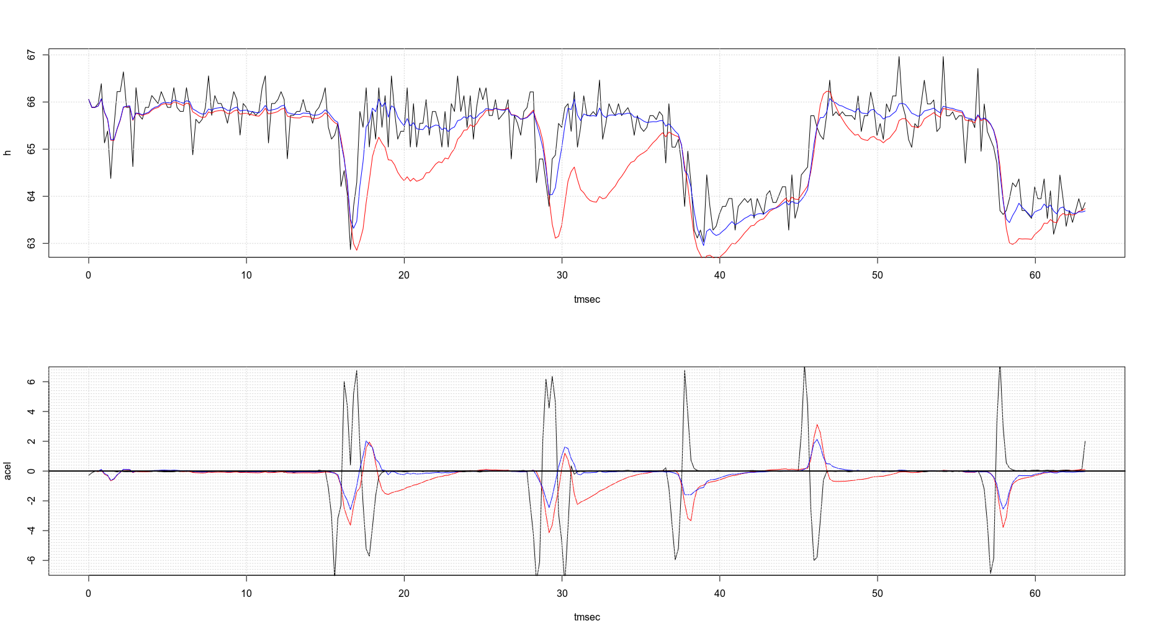
There’s one more problem in trusting the accelerometer so much: The centrifugal forces generated during a banked turn change the direction of the gravity force and sum to it making up an apparent load as when you are climbing.

Lowering the weight of the accelerometer readings over the barometer readings we reduce drift and rebounds at the cost of increasing noise. See the figure below.

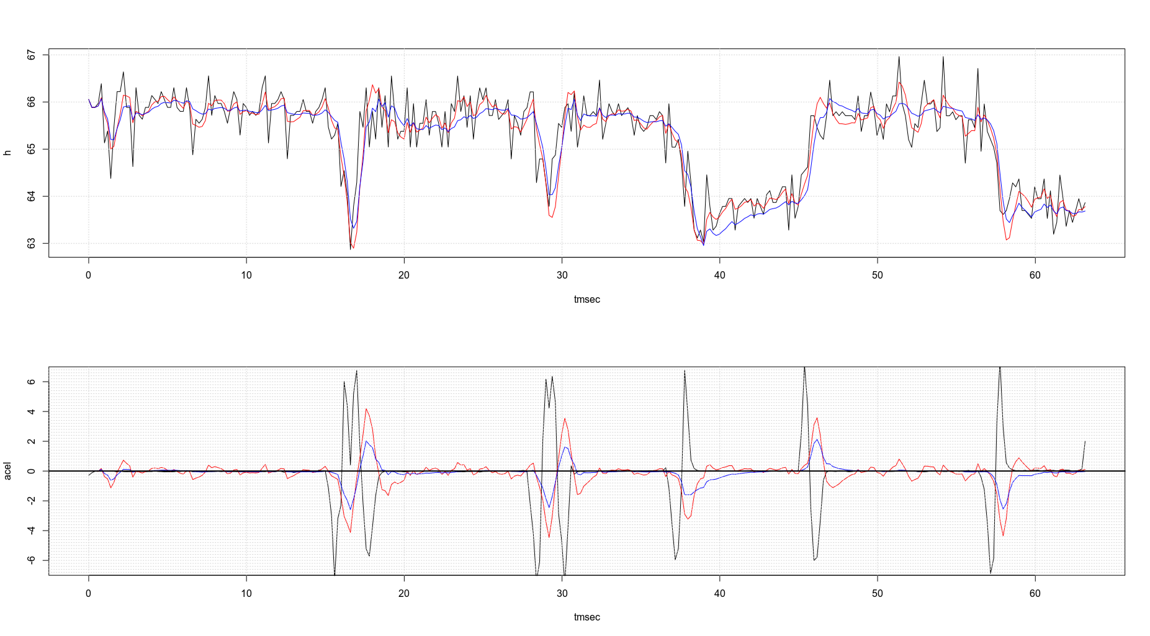
The blue line corresponds to the output of our lag-free algorithm. Using it we can reduce RMS noise in the vertical speed to 0.07 m/s with a fairly acceptable delay.