Glide farthest

Las teorías tradicionales para el cálculo de la velocidad de planeo máximo no sirven cuando el curso de vuelo no coincide con el rumbo. Prácticamente ningún instrumento tiene esto en cuenta cuando calcula la velocidad de planeo máximo.

La curva polar de un planeador es la tasa de caída del planeador en función de la velocidad aire en aire estable \([f(v_a)]\). Si la masa de aire no es estable sino que desciende a una velocidad [s] la tasa de caída indicada por el vario será \(\color{black}S = f(v_a) + s \). Si expresamos la tasa de caída [S] y la velocidad tierra \( [v_g] \) en las mismas unidades la tasa de planeo se calcula como:

$$\color{black}L/D=\frac{v_g}{S}$$

Igualando a cero la derivada de la tasa de planeo respecto a la velocidad aire obtenemos la condición de planeo máximo para la velocidad aire.

$$\color{black}f’(v_a^{opt}) = \frac{dv_g}{dv_a} \cdot \frac{S}{v_g^{opt}}$$

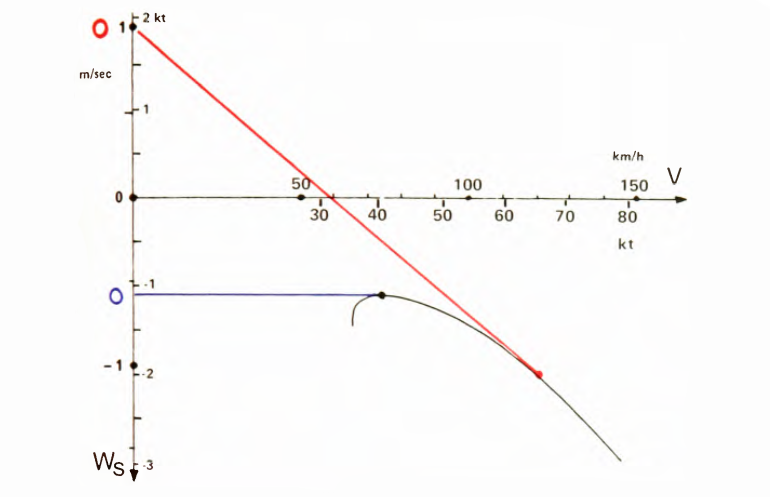
En este contexto es fundamental entender que la velocidad tierra depende de la velocidad aire. Si no hay movimiento horizontal de la masa de aire \(\color{black}v_g=v_a \) por tanto \(\color{black}dv_g/dv_a = 1 \). La velocidad de planeo óptimo se obtiene gráficamente como la tangente desde el origen a la curva polar desplazada verticalmente una cantidad [s]. En la gráfica tomada del magnífico libro Cross-country soaring, Helmut Reichmann desplaza el origen de coordenadas hacia arriba en lugar de desplazar la curva hacia abajo. Podemos ver que la velocidad de máximo planeo en una masa de aire que desciende a 1 m/s son 120 km/h. La tasa de planeo es 16:1 y la tasa de descenso indicada por el vario 2.05 m/s. Obsérvese que para llevar a cabo este cálculo es necesario conocer la velocidad de descenso de la masa de aire [s] y para ello hay que conocer la velocidad aire de nuestro planeador (anemómetro) y despejar \(\color{black}s = S - f(v_a) \) utilizando la tasa caída indicada por el vario.

Si hay un movimiento horizontal de la masa de aire [w] en la misma dirección de nuestra velocidad tierra entonces \(\color{black}v_g = v_a + w \) por tanto \(\color{black}dv_g/dv_a = 1 \). La curva polar debe desplazarse también horizontalmente una cantidad [w] antes de trazar la tangente. Obsérvese que esta cantidad se obtiene fácilmente si conocemos la velocidad aire y llevamos un gps que nos de la velocidad tierra haciendo: \(\color{black} w = v_g - v_a \)

---

Hasta aquí la teoría tradicional es suficiente pero en el caso más general la dirección del viento no coincide con la de la velocidad y por tanto tampoco coinciden el course and the bearing. The course is our glider’s heading, and the bearing is our flight direction over the ground. Ambos vienen indicados por las direcciones de las flechas verde y roja de la figura superior mientras que sus longitudes indican la velocidad aire y la velocidad tierra respectivamente. Ambas son magnitudes vectoriales y por tanto constan de intensidad y dirección. El viento es otra magnitud vectorial. Para obtener el viento ahora debemos aplicar la misma ecuación que vimos arriba pero usando magnitudes vectoriales. Una sonda de viento sólo es capaz de darnos la intensidad de la velocidad aire pero no el curso así que debemos contar también con una brújula. Sólo entonces podremos obtener la intensidad y dirección del viento. \(\color{black} \vec{w} = \vec{v_g} - \vec{v_a} \)

En este punto estaremos tentados de utilizar el viento meteorológico obtenido por el instrumento de vuelo con el método descrito en this article pero sería un error tan grande como sustituir [s] por la tasa de caída promedio de los últimos 20 minutos. La velocidad de máximo planeo debe tener en cuenta las ráfagas de viento tanto horizontales como verticales y no el viento meteorológico.

Utilizando un poco de trigonometría se puede demostrar que ahora: $$\color{black}v_a^2=w^2+v_g^2-2w\cdot v_g\cdot cos\beta ,\qquad \frac{dv_g}{dv_a} = \frac{v_g - w\cdot cos\beta}{v_a}$$

Una vez calculada la velocidad aire de planeo máximo, si esta es menor que la velocidad aire indicada por el anemómetro, el instrumento de vuelo nos indicará que reduzcamos la velocidad y viceversa.